It’s been a complicated few months. I moved across the country from Seattle to the DC area, and have a somewhat new role at work as a PI on a big, long-term project. Anyway, I’ve been busy. Not so busy I don’t have time to post on bluesky (which people can apparently now access without a login), but I still haven’t had much time to sit down, run the models, and write long-form.
I lived here about a decade ago (2011-2012). Funny enough, I originally came up with the application of information equilibrium to economics at that time1. Pulled up my old mathematica notebooks where I was drafting what would become this paper (also on SSRN)2.
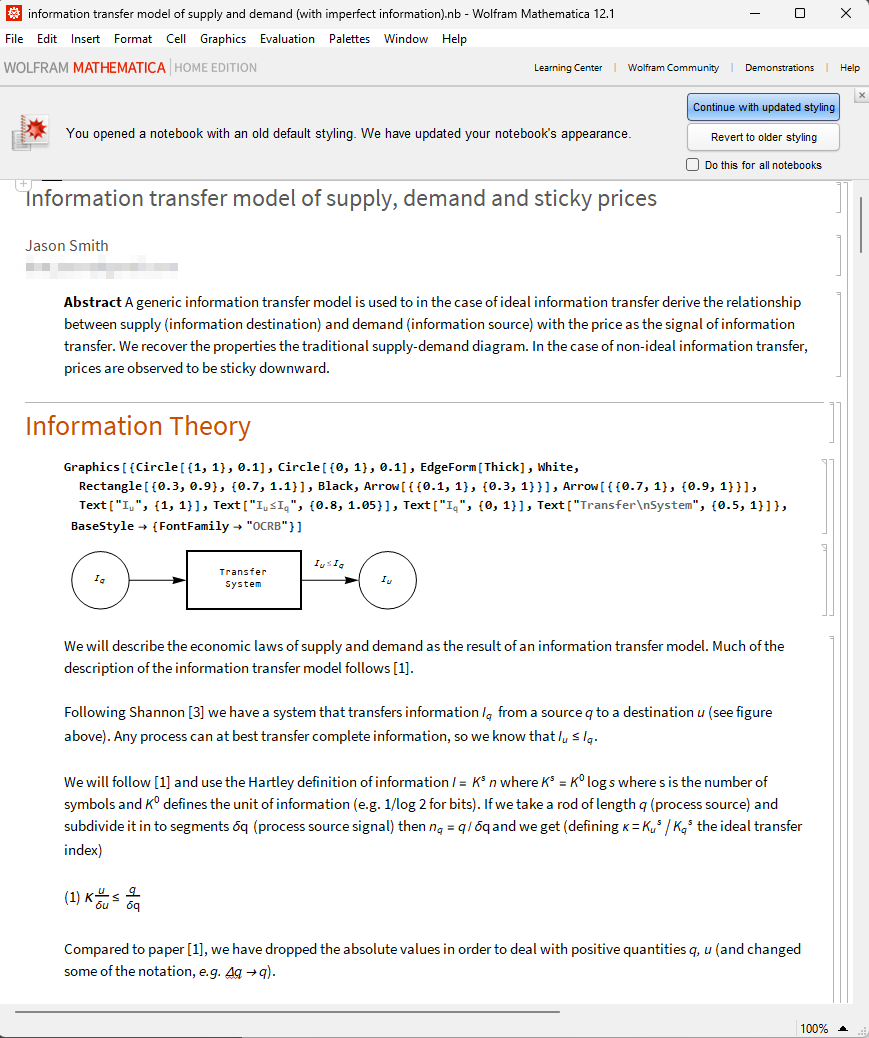
This post isn’t really going to be a return to blogging3; however, I plan on doing a comprehensive labor market update with next Friday’s employment situation report. In the mean time, I thought I’d link to a couple of other substack posts that caught my eye.
I love Dan Davies’ work and pre-ordered his new book. His substacks always feel like you managed to catch one of the smartest, busiest people in your company in the elevator and they start an interesting conversation that suddenly ends when they get to their floor. This recent one had a great paragraph that would work as the problem set up in a pitch for the information equilibrium approach:
But it’s information theory applied to a context of “extremely connected, extremely complex” systems, where the idea of measuring the amount of information, as a number of bits, is ridiculous. The numbers are absurdly huge, because connective complexity multiplies up rather than adding up. So the fundamental law just becomes “make sure that one unimaginably huge number that you have no way of measuring is greater than or equal to another unimaginably huge number that you have no way of measuring”. Which isn’t very helpful.
Claudia Sahm’s “rule” seems like one of the few true advances in macroeconomic “stylized facts” since Okun4; here she is talking about more than just the math — including the new paradigm for automatic stabilizer policy that could be enabled by good metrics.
As I said above — I hope to get back to blogging with an analysis of the labor market data coming out at the end of next week. As a teaser, here’s the forecast of headline CPI inflation from March of 2022 (two years ago!) using vintage data with the most recent release from earlier this month in black:
Looks like we’re basically back to equilibrium. The monte carlo (thin gray lines) shows how we might be seeing a bit of upward bias, but for the most part it’s 2010 again.
It germinated from some information theory work I was doing along with a visit to IARPA while Jason Matheny was running the ACE program. I later called him up to pitch information equilibrium as a way to construct metrics for prediction markets, and he told me that I should put it in front of some academic economists (eventually did, at UW). Anway, he’s done well for himself since then.
Just noticed that my “newest” paper on SSRN (that is laughably more than six years old now) reached 1000 downloads recently.
I’m still considering whether I should continue here in the light of some of the issues with Substack. They’ve apparently acted to remove some of the more egregious Nazis, but I’m not fully convinced the site will be a good place to devote a significant resources.
I actually put together a forecasting tool that is formally similar to the Sahm rule; instead of triggering automatic stabilizers, the threshold (which is in log, not linear scale) would trigger the model to switch priors from an equilibrium log-linear decline in u to a logistic non-equilibrium shock. On the other hand, at least from the point of view of the dynamic information equilibrium model, Okun’s law isn’t so much a deep structural relationship but an empirical regularity that seems ok only because it changes slowly.







Glad you’re still writing!