What does it mean when we say money flows?

Last night through this morning, I butted into an exchange on Twitter about the flow of money between Steve Roth and Noah Smith (who promptly booted me from whatever strange nonsense he wanted to blather on about ... you can't send a signal with wavefunction collapse and it has nothing to do with money flow [economists: stop talking about quantum mechanics]). It brings up some interesting points. Steve started with the observation that money appears to teleport from one account to another -- there is no "flow" per se. Noah said this was just like water which I assume was an attempt at Ken M style trolling because it makes no sense.

Anyway, here is an animation of dots being instantly debited from one account (box) and credited to another; I know because I wrote the Mathematica code that does it (feel free to email me via the box on the sidebar for a copy):

It's from this post. There is strict accounting (the number of dots is constant, and one dot taken from one box is exactly matched by a dot added to another). Then Steve asked the question that you'd hope to get if you were teaching this stuff as a class:

Which raises the interesting (for me...) Q: when I send you money, how far does it "move"?

This is an interesting question and in the animation above there is an explicit answer: it moves one box in one time step. In real life, if you gave several people a large amount of money, you could measure how fast it moves from one node in the network to another. One bought dinner here; another bought a record there. The restaurant and music store paid their employees the next Thursday, but the wait staff took home their tips that night and one picked up some groceries. It possibly changed forms during this journey from cash from an ATM or a deposit at one. This data would be an input to a bottoms-up measurement of money velocity.
These measurements determine the flow rate of money in an economy analogous to the flow rate of the wave in the animation above. There's another picture from that same post -- it shows the density at a single site:

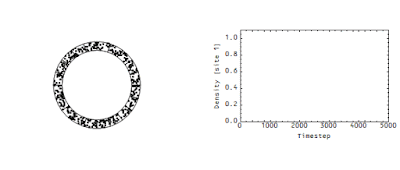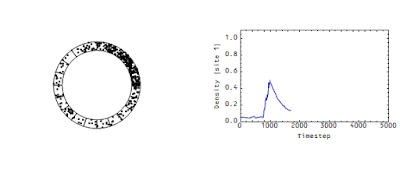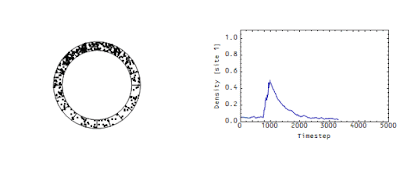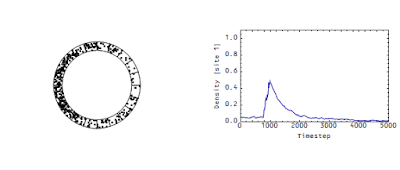
Note that there's a "decay constant" (of about 500 time steps) -- this decay constant is directly related to the speed of the flow in the first animation. The faster that wave moves in the first animation, the faster the density would decay in the second animation.
I hesitate to bring it up again, but this is exactly what I was talking about when I criticized stock-flow consistent models (Steve also brought up "accounting" approaches).
Even though the accounting is exact in the model above, I could make the wave travel faster or slower (and therefore the decay happen faster or slower) by changing the size of the debits and credits or changing the number of transactions per time step. The velocity of the wave is a free parameter not established by pure accounting. In the linked post, I called that free parameter Γ and was promptly attacked by the stock-flow consistent community for heresy.
So where does this parameter come from? Where does velocity come from? Where does my freedom come from when Nick Rowe says:

But velocity is not just an accounting relationship between flows and stocks. I can choose the velocity of circulation of the money I hold.

Let's consider a set of accounts on a network: I buy something from you, you buy something from someone else, etc. all in a chain (time steps t are vertical, and accounts a are horizontal):

Now, what happens if I do this:

I made the accounts farther apart and the time steps closer together. In terms of accounting? I did nothing. It's just a graphic design choice. That's because these accounting boxes have nothing to do with each other in time and space. However, I've implicitly related them to each other because the boxes "next to" each other are in a sense closer to each other. There is some kind of "connection" between boxes (two are shown in blue):

How do I measure distance diagonally? How is one time step related to one account step? Well, much like how I could make any graphic design choice, I can choose any relationship between a time step Δt and an accounting step Δa (I could even make Δa = Δa(t) change as a function of time -- an expanding accounting universe). There's a free parameter that comes out of this two-dimensional space time (for flat space). In physics, it's called the speed of light (c). The space steps Δx are related to time steps Δt such that distance Δs is measured with some function
Δs² = f(Δx, c Δt) = c² Δt² - Δx²
... at least for the those of us on the West Coast.

This is what was so frustrating about the stock-flow argument. The metric was assumed to be analogous to

Δs² = f(Δx, c Δt) = Δt² + Δx²

as if it was a fundamental accounting error to assume otherwise. Frequently physicists do assume h = c = 1. But then we measure everything in terms of energy or distance. One Fermi is not just a distance but also a time and both are the same as 1/197 MeV (inverse energy) which is also about 1/400 electron masses. That's only because the theory of relativity exists relating energy, matter, space, and time. You could do this in stock flow models -- assuming a new fundamental constant Γ = 1 dollar/quarter -- but then you'd have to measure time in terms of money. A year is not 4 quarters, but rather 4 dollars-1.

Stock flow consistent analysis is not the special relativity of economics and there is no such fundamental constant as Γ. The accounting "metric" changes over time (those time steps can seem pretty fast when there's a recession happening).