Wage stickiness is an entropic force
David Glasner has a post up about the hegemony of new classical economics through "microfoundations"; this latest take put the question in an interesting way that goes well with what I've been thinking about lately:
In chapter 19 of the General Theory, Keynes struggled to come up with a convincing general explanation for the failure of nominal-wage reductions to clear the labor market. Instead, he offered an assortment of seemingly ad hoc arguments about why nominal-wage adjustments would not succeed in reducing unemployment, enabling all workers willing to work at the prevailing wage to find employment at that wage. This forced Keynesians into the awkward position of relying on an argument — wages tend to be sticky, especially in the downward direction — that was not really different from one used by the “Classical Economists” excoriated by Keynes to explain high unemployment: that rigidities in the price system – often politically imposed rigidities – prevented wage and price adjustments from equilibrating demand with supply in the textbook fashion.
Why, in a recession, don't people take wage cuts to clear the labor market?
I think I have an answer: entropy. There is nothing stopping anyone from making the adjustments, it's just highly unlikely that the adjustments will be made (or another way, it is highly unlikely for the economy to find itself in a state where the adjustments have been made). People are pushing against the headwind of an entropic force -- an entropic force that is known by its economics discipline name of sticky wages.
That's why it would be hard to come up with a microfounded explanation for the lack of nominal wage reductions -- there is no microeconomic reason. Sticky wages disappear as you get a smaller and smaller economy, going from macro down to the micro level. A single glue molecule is not sticky and individual molecules do not undergo diffusion.
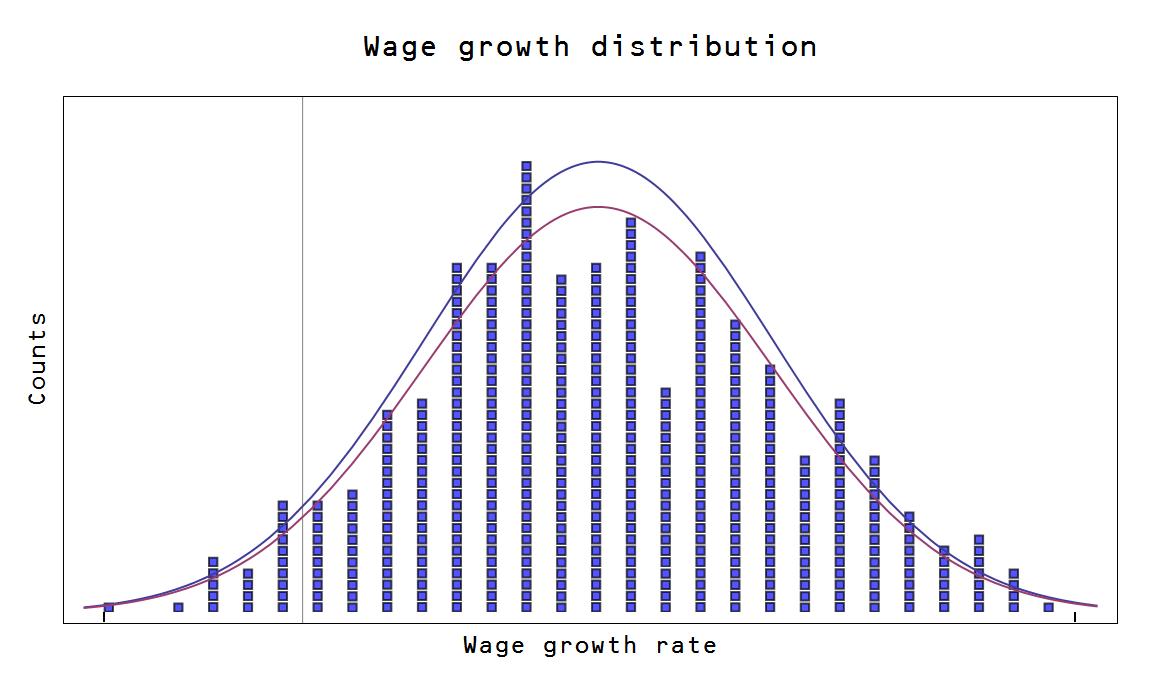
Let me try an explanation. Nominal wages (NW) are remarkably correlated with NGDP -- in fact, NGDP = 2.1 NW to a very good approximation. So lets assume that nominal wage growth in a given industry (or company) is proportional to [the growth of] that industry's contribution to NGDP. We can then borrow the picture from this post to talk about the distribution of wage growth:

The mean and variance of this distribution is set by macroeconomic variables -- like NGDP and the money supply [1].
If one person takes a nominal wage cut, he or she would move along the red arrow to a position on the negative growth side to the left of the vertical line. It doesn't impact the shape of the distribution too much. However, if lots of people do it, you'd end up with a different distribution:

If this were a thermodynamic variable, the particles on the left side would "experience" an entropic force to return to the original distribution .. because that original distribution represented the most likely configuration consistent with the macro scale variables. The individual particles wouldn't actually feel any force, they'd just end up by random chance back in the most likely configuration.
Well, in the information transfer picture, the labor force would experience that same entropic force. That is to say, they wouldn't feel anything themselves -- in aggregate the labor force would just keep the same distribution of nominal wage growth. Some people would move up, some down. The distribution of wages would have a tendency to stay the same since they are set by macro variables, few people end up with negative nominal wage adjustments to an exogenous shock and wages appear to be "sticky" [2].
Right now you might be saying: "Wait, how can a recession happen at all in this picture?" There are two ways. One is to throw people out of this distribution in proportion to the distribution itself (subtracting a Gaussian from a Gaussian with the same mean and variance is just a re-normalized Gaussian with the same mean and variance). In this case unemployment spikes and you get a one time drop in NGDP that reduces the average growth rate going forward (see footnote [1]). This picture is below:
This mechanism predicts that the distribution of the wage growth of the about-to-be unemployed before the layoffs is roughly the same as the wage growth distribution of the employed before the layoffs. That is to say most people laid off would have had the average wage growth of the employed before the layoffs -- that people with low wage growth or high wage growth prior to the layoffs are not over- or under-represented in layoffs.
The second way is for the market to stop transferring information, prices stop detecting the information flow and nominal wage growth freezes (goes to zero -- see e.g. here [link fixed 10/3/2014]). If I(D) is the information source (demand) and I(S) is the information destination (supply), then this represents a case where I(S) < I(D). It could be described as a coordination failure (the information in peoples' expectations is lost as their inconsistent plans fall apart) or incorrect expectations which lead to information loss.
The first way, we maintain I(S) ≈ I(D); second way is a market failure -- I(S) ≠ I(D). My opinion is that a little of both happens. Its a bit like trying to get the price tag sticker [2] off of birthday card and ripping the card in the process. Your fight with entropy is partially successful and partially system failure. In this analogy, the economy is the card, the soon-to-be unemployed are the price sticker and you are acting as the economic shock to the system.
Footnotes:
[1] In particular, using the partition function approach, the mean of the wage growth distribution is ~ log NGDP/log M and the variance is ~ 1/log M.
[2] An entropic force we experience in our everyday lives is the stickiness of glue. There is literally nothing you are fighting against when you try to peel a price tag off something ... except entropy.



