Unemployment rate step response over time

One of the interesting effects I noticed in looking at the unemployment rate in early recessions with the dynamic equilibrium model was what looked like "overshooting" (step response "ringing" transients). For fun, I thought I'd try to model the recession responses using a simple "two pole" model (second order low pass system).

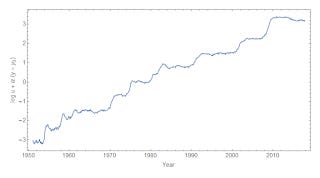
For example, here is the log-linear transformation of the unemployment rate that minimizes entropy:

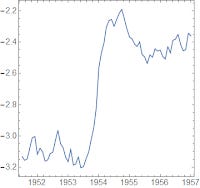
If we zoom in on one of the recessions in the 1950s, we can fit it to the step response:

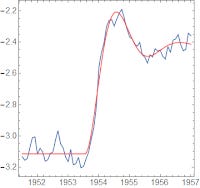
I then fit several more recessions. Transforming back to the original data representation (unemployment rate in percent), and compiling the results:

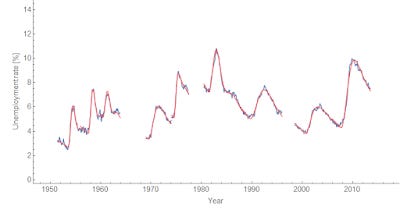
Overall, this was just a curve fitting exercise. However, what was interesting were the parameters over time. These graphs show the frequency parameter ⍵ and the damping parameter ζ:

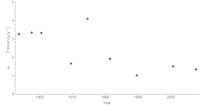
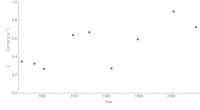
Over time, the frequency falls and the damping increases. We can also show the damped frequency which is a particular combination of the two (this is the frequency that we'd actually estimate from looking directly at the oscillations in the plot):

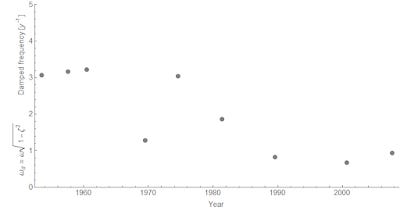
With the exception of the 1970 recession, this shows a roughly constant fairly high frequency that falls after the 1980s to a lower roughly constant frequency.
At this point, this is just a series of observations. This model adds far too many parameters to really be informative (for e.g. forecasting). What is interesting is that the step response in physics results from a sharp shock hitting a system with a band-limited response (i.e. the system cannot support all the high frequencies present in the sharp shock). This would make sense — in order to support higher frequencies, you'd probably have to have people entering and leaving jobs at rates close to monthly or even weekly. While some people might take a job for a month and quit, they likely don't make up the bulk of the labor force. This doesn't really reveal any deep properties of the system, but it does show how unemployment might well behave like a natural process (contra many suggestions e.g. that it is definitively a social process that cannot be understood in terms of mindless atoms or mathematics).