The price adjustment equation and information equilibrium

Ian Wright and I share a love of Mathematica, but after reading his [1] recent post and one that it references I think we might share a framework. In fact, I may want to rewrite the derivation of the information equilibrium relationship using his derivation of his [2] price adjustment equation. Here is Ian's derivation (that I LaTeX-ed up a bit):

We need to translate this price adjustment strategy into something a bit more precise. Let $\Delta s$ be the change in the stock of corn (during a short period of time). And let $\Delta p$ be the change in the price of corn. We want to define $\Delta p$ (the price adjustment strategy) in terms of $\Delta s$ (the indicator of market demand relative to our level of production). 

Clearly, if our prices are huge, in absolute terms, we should make bigger price adjustments compared to when our prices are tiny. So we want $\Delta p$ to be proportional to $p$. We write this as (i) $\Delta p \propto p$. 

And, if our stock decreases then we should raise our prices (and vice versa); or, in other words, (ii) $\Delta p \propto - \Delta s$. 

Finally, we should set the price of corn astronomically high if we’re completely running out of stock; that is, (iii) $\Delta p \propto 1/s$. (This implies that, in the hypothetical situation that our stock reaches zero, then the price of corn is infinity — meaning, quite correctly, that no amount of money can buy corn.) 

Putting (i), (ii) and (iii) together we get the price adjustment equation: 

 $\Delta p = - \eta \Delta s (p/s)$

where $\eta$ is a constant of proportionality. We should give $\eta$ a name. Call it the elasticity of price with respect to excess supply ...

This price adjustment equation can be derived from the information equilibrium condition. I went through this derivation before here in the context of stochastic processes, but just let me repeat it here with the notation changed a bit to match up with Ian's. Let's start with the information equilibrium condition

$$
p \equiv \frac{\Delta d}{\Delta s} = k \; \frac{d}{s}
$$

where $s$ is the stock, and $d$ is the demand for that stock. In the compact information equilibrium notation I sometimes use, I write this condition as $p : d \rightleftarrows s$ (where $p$ is the "detector"). I also usually take the continuous limit $\Delta x \rightarrow dx$. Varying $p$ we obtain:
$$
\Delta p = k \left( \frac{\Delta d}{s} - \frac{d}{s^{2}} \Delta s \right)
$$

$$
\frac{\Delta p}{p} = \frac{\Delta d}{d} - \frac{\Delta s}{s}
$$

In the last line, I re-used the information equilibrium condition (i.e. $p = k \; d/s$). If demand is constant or at least large compared to changes (i.e. $d \gg \Delta d$), then the last line becomes:
$$
\Delta p = - \Delta s \frac{p}{s}
$$

which is Ian's price adjustment equation with $\eta = 1$. The information equilibrium version has $\eta = 1$ because of the original scale invariance it manifests. However, Ian's equation follows from a slightly more general information equilibrium condition:
$$
p \equiv \frac{\Delta d}{\Delta s} = k \; \frac{d^{\zeta}}{s^{\eta}}
$$

which becomes:

$$
\frac{\Delta p}{p} = \zeta \; \frac{\Delta d}{d} - \eta \; \frac{\Delta s}{s}
$$

so that with $\Delta d \ll d$, we have

$$
\Delta p = - \eta \Delta s \frac{p}{s}
$$

Ian's price adjustment equation is both more general (it doesn't require $\eta = 1$) and less general (it doesn't account for changing demand $d$ for stock $s$, i.e. that $\Delta p = f(\Delta d, \Delta s)$). Also, whether or not scale invariance is an important aspect of economics is not known, so the more general equilibrium condition may be better empirically. Ian's derivation points to at least one way the information equilibrium condition may be generalized. 
Actually, Ian asked via Twitter while I was writing this post:

One of the problems when specifying dynamic adjustment is there are too many reasonable equational forms. Does your approach help here?

One could say the information equilibrium approach helps by connecting to underlying information theory thereby restricting the number of possible equation forms. The scale invariance is doing a similar thing (and could be used to build generalizations a la effective field theory (or see here)). It does involve viewing the communication channel the market represents slightly differently. In the traditional view, the price contains information received from supply and demand; in the information transfer view, the "communication" is between supply and demand (usually I put demand as the transmitter and supply as the receiver).

Do we believe in scale invariance or that the market represents an information processing system? If yes, the information equilibrium approach does help control the reasonable forms of equations (actually, this was part of this blog's mission statement). But if we think these other considerations aren't important, then they're just ad hoc restrictions.

I personally believe the information theory framing is very useful and that scale invariance may be one of the most important (defining, even) properties of economics as a dynamical system (actually, "money" might be abstractly viewed as something that exists to maintain that scale invariance). However I understand this is probably a minority view. Still, it's not like Ian and I are on completely different pages here. (His simulations also manifest some information equilibrium relationships, and I think we have some of the same ideas about statistical equilibrium.)

*  *  *

A quick aside: Ian's price adjustment equation could be seen as an information equilibrium relationship in its own right where price is in information equilibrium with (one over) the stock. Ian's equation is:

$$
\frac{\Delta p}{\Delta s} = - \eta \; \frac{p}{s}
$$
which we can say is (taking $s \rightarrow 1/s'$):
$$
\frac{\Delta p}{\Delta s'} = \eta \; \frac{p}{s'}
$$

Which I'd write as $p \rightleftarrows 1/s$ or $p \rightleftarrows s'$ in the compact notation. Dealing with the minus sign is necessary because $\eta$ here represents an information transfer index and is necessarily positive as it the the ratio of the information content of a selection from the distribution of $p$-states to the information content of a selection from the distribution of $s'$ states.
*  *  *

Ian also says in the post [2] above

There’s a simple moral to this story: price adjustment alone does not solve the coordination problem.

Emphasis in the original. This something I agree with. In the information equilibrium view, and in an ideal market, prices simply measure changing demand and changing supply (we call it a "detector" of information flow and it's a ratio of the changing information in the demand distribution to the changing information in the supply distribution). However, the overall story is much more complex because there is no real guarantee e.g. all of the information in the signal sent by a change in the demand distribution is received by the supply distribution. This results in our information equilibrium condition being only a bound:
$$
p \equiv \frac{\Delta d}{\Delta s} \leq k \; \frac{d}{s}
$$

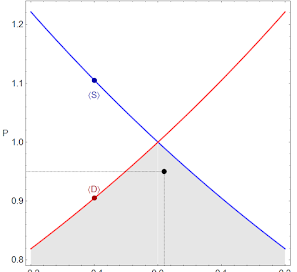
This is still useful via Gronwall's inequality, but leads to a much more nuanced take on the "information aggregation" problem the market is used to solve versus the "allocation" (coordination) problem the market is used to solve. It also leads to viewing supply and demand diagrams as "bounds" with the real price falling somewhere in the lower triangle:

and (for example) price time series being seen as stochastic paths constrained by the bounds.
*  *  *
PS On a more speculative topic, information equilibrium might be related to Generative Adversarial Networks in machine learning.