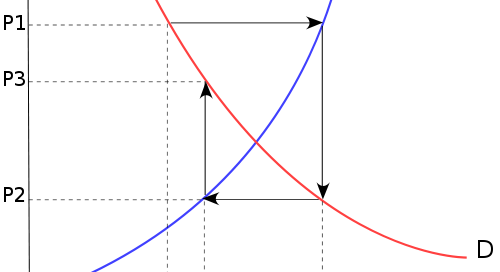
The cobweb model

In writing the posts about expectations I stumbled across the cobweb model of how expectations can impact prices in the short run, creating periodic fluctuations and volatility. The basic idea is that there are two possibilities for a series of price adjustments, convergent and divergent [from Wikipedia]

If we take the price elasticity conditions $e^{s} < |e^{d}|$ for convergent and $e^{s} > |e^{d}|$ and use the information transfer model for the elasticities (convergent case):

$$
\frac{\kappa Q_{0}^{s}}{Q_{ref}^{s}} \lt \left| - \frac{Q_{0}^{d}}{\kappa Q_{ref}^{d}} \right|
$$

If we assume an equilibrium market price $P_{0}$, then we can say the information source $Q_{0}^{d}$ and destination $Q_{0}^{s}$ are equivalent as well as the initial conditions ($Q_{ref}^{x}$)
$$
Q_{0}^{d} = \kappa P_{0} Q_{0}^{s}
$$

$$
Q_{ref}^{d} = \kappa P_{0} Q_{ref}^{s}
$$

we obtain the conditions:

$$
\frac{\kappa Q_{0}^{s}}{Q_{ref}^{s}} \lt \frac{\kappa P_{0} Q_{0}^{s}}{\kappa^{2} P_{0} Q_{ref}^{s}}
$$

$$
\rightarrow \;\;\; \kappa \lt \frac{1}{\kappa}
$$

$$
\rightarrow \;\;\; \kappa^{2} \lt 1
$$

for the convergent case, and analogously

$$
\kappa^{2} \gt 1
$$

for the divergent case. Basically the convergence and divergence is set by the value of $\kappa$.