Summer blogging recess (and no-go theorems)

I have a bunch of things to attend to over the next month or so, so there will be few (if any) posts. I plan on working (the real job), taking a couple of trips (work- and non-work-related), thinking about a problem Cameron Murray suggested, and finishing up the first draft of the book (see here; I've been spending some time away from the draft, hoping to come back to it with new eyes).

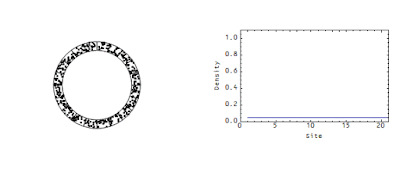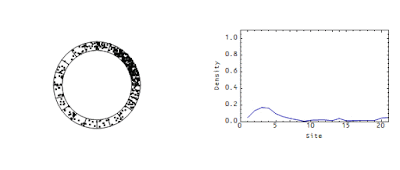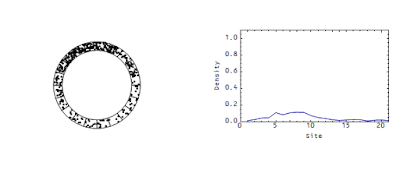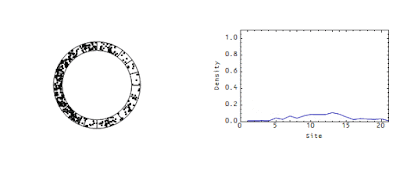
I will also continue to be baffled by the stock-flow accounting advocates (see comments here and here). It seems more and more to be a paradigm akin to market monetarism to me. Market monetarism exists in order to deny the effectiveness of fiscal stimulus [as a primary policy tool]; Stock-flow accounting exists to deny the existence of any weakly-emergent properties of macroeconomies. Everything they seem to say is inconsistent with this picture:

Not this model, mind you, but the existence of this picture. The weakly-emergent travelling wave cannot exist -- even though this kind of weakly-emergent structure is perfectly consistent with strict accounting of the variables.

All I get in response are attempts to teach me accounting! Trust me -- accounting "theorems" don't quite rise to the level of Stokes' Theorem; this stuff is not complex except in vocabulary. I have degree in math with particular emphasis in topology and differential geometry. The discrete point set on which accounting is defined can't be more complex that the typical topology of the Cantor set. However, the main issue is that "you don't understand accounting" isn't particularly responsive to the question: Why are there no weakly-emergent (e.g. field) quantities in systems that obey accounting principles?

Is there some proof of this? It would be some kind of no-go theorem for certain covering spaces of a space defined by a set of functions on some discrete point set, network, or connected intervals. This is of course not generally true: all of solid state electronics is a counterexample, as well as things like temperature and pressure.

There would have to be something specific about the accounting equations that prevents this. However, accounting operators aren't exactly elliptic differential operators, so I have difficulty imagining a no-go theorem arising from addition and multiplication.

This may sound like I' trying to win an argument by bringing up a lot of high level mathematics, but that's actually what's at issue. Denying weakly emergent quantities is a pretty high level mathematical question about the properties of discrete spaces. I can't imagine it can be answered by double entry bookkeeping.