Stuff measured by GDP and the emergent representative agent

I am turning one of my comment responses into a post because I think it has broader interest and relates to this post on the emergent representative agent. Commenter Jamie discusses what does and doesn't contribute to GDP -- a discussion that was briefly the topic of the blogs earlier this summer.

Let's count Jamie's examples that contribute to GDP as "consumption" C and those that don't as "other". If we have two time periods consumption goods 1 and 2 the consumption by people is going to be constrained by

C₁ + C₂ ≤ GDP

The actually realized consumption in an economy is likely to be less -- if C₁ = σ₁ and C₂ = σ₂, then we have:
σ₁ + σ₂ < GDP

or

σ₁ + σ₂ + ɛ = GDP

where ɛ is that "other stuff" that is not a part of GDP (ɛ is the distance from the budget constraint line). I drew a picture of this scenario here:

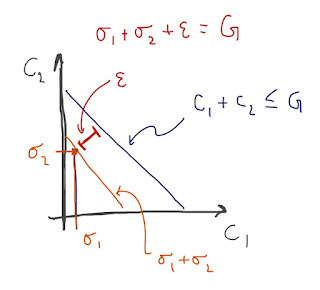
In the two period good case, the ensemble average would give you a point in the middle of the triangle with ɛ > 0 and σ₁ + σ₂ < GDP.
However! (And this is pretty neat -- it depends on the mathematical properties of higher dimensional spaces.)
If you have a lot of consumption periods goods C₁, C₂, C₃, ... Cn subject to the budget constraint Σ Ci ≤ GDP, then the ensemble average (expected value) is
ɛ' + Σ σi = GDP

with ɛ' ≈ 0 simply because most of the points in the higher dimensional space are near the budget constraint (now a hyperplane). This scenario is illustrated here:

The ensemble average (the "representative agent" at the blue point) spends all of their consumption on things that count towards GDP, but individual agents (e.g. σi) do not necessarily do so.

Update 9/13/2015:

I changed the problem to be a single time period and instead had i index different consumption goods. The intertemporal version doesn't really illustrate the point I was trying to make.