Recoveries do grow old; they just have an uncertain lifetime

There was an article out of the SF Fed that seems to suggest that post-WWII recoveries do not "grow old". They assume a Weibull distribution for the PDF for post-WWII recovery lengths (and I'm assuming for the pre-WWII recoveries as well) and then observe that the hazard function is "nearly flat" (has no time scale). The implication is that post-WWII recoveries don't "grow old" and end in recession.

I wasn't entirely convinced by that argument -- the reason for a hazard function to not be flat is that it has not only a well defined mean lifetime (scale), but additionally a very low variance. Those properties result in a strongly peaked PDF which leads to a sharply increasing hazard function over a short period of time. Because of the graph limits shown in the SF Fed article, it makes it look like the pre-WWII hazard function shoots up forever, while the post-WWII hazard function gradually increases. The pre-WWII hazard function actually has to level off after that initial increase -- which isn't shown.

The real argument that post-WWII recoveries don't grow old is that they are scale-free -- lack a well defined lifetime. However the use of a Weibull distribution for the post-WWII recoveries assumes they do have a lifetime (i.e. Weibull distribution has time scale).

But you can't assume a different type of distribution for the post-WWII recoveries than for the pre-WWII recoveries because you don't have very much post-WWII data. In a sense, you're kind of stuck. The data is mostly pre-WWII and a Weibull distribution looks appropriate for that. That means you're stuck with a Weibull distribution with different parameters for the post-WWII data [1] -- and therefore stuck with a lifetime.

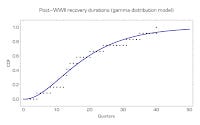
I basically re-did the analysis using a gamma distribution to find out the scales (mean and variance). I fitted the empirical CDFs to regularized gamma functions and extracted the distributions for pre-WWII, post-WWII and used a sum of the distributions to represent all the data. Here are the resulting fits:

And here are the resulting PDFs:

The two distributions have means of 2.2 years (pre-WWII) and 4.8 years (post-WWII), but the big difference is in the variance. The square root of the variances are 1.0 years and 3.1 years. The post-WWII distributions are quite spread out. The result is a "flat" hazard function:

But post-WWII recoveries still "grow old" (after about 4.8 years), they just don't have a well-defined lifetime (± 3.1 years). As the current recovery is about 30 quarters long, so we'd expect about a 9% chance of a recession in the next quarter. But since the variance is so high, it takes 10 years (40 quarters) to reach a 99% chance of a recession (at least with this model):

...

Footnotes

[1] Statistical tests pretty definitively show that the post-WWII data is drawn from a different distribution than the pre-WWII data. We know that the distribution changed, but we don't really have enough data to pick a new kind of distribution -- even though that might be warranted.