Production possibilities and the slope of the supply curve

There was a discussion on the blogs about teaching the Production Possibilities Frontier [PPF] (or curve) for two goods (say, Apples and Bananas) in introductory economics classes. Brad DeLong started it; Paul Krugman joined in. Then there was more from DeLong.

Nick Rowe went over it awhile ago in a post, and commented on DeLong's first post above, saying:

How can you (easily) explain (e.g.) why supply curves slope up without using a (curved) PPF?

Which is similar to what he said in his post:

Which means the PPF is now curved, and bowed out. ... Which means that the supply curve of apples will slope up.

Now I reconstructed the PPF using an information equilibrium model in this post based on Rowe's post. It turns out the PPF is a level curve of the production possibilities surface constructed from the quantity-weighted sum of the supply curves (surfaces) for the two goods. Here are the supply and demand diagrams (assuming the markets are independent and e.g. the supply curve line becomes a plane):

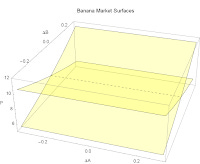
Here are the supply surfaces together:

And here is their quantity weighted sum -- the production possibilities surface [PPS] -- (with level curves, aka various PPF's):

If you take flat supply surfaces:

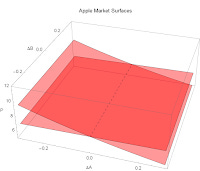
and take the quantity weighted sum, you get straight lines for your PPF's:

which is exactly how it works at Nick Rowe's post. But I did want to add a bit here. Nick Rowe's comment at DeLong's blog seems to suggest that a curved PPF "explains" the upward sloping supply curve. However, since those PPF's are level curves of the quantity-weighted sum of the two supply surfaces, the idea that "the PPF bows out" (the level curves of the PPS are bowed out) and the "supply curve for a single good slopes up" (i.e. the PPS has curvature) are not logically independent of each other. That is to say, they mean the same thing -- there is no knowledge added to a bowed out PPF to makes it lead to a upward sloping supply curve.
The curvature of the PPS is determined by weighting a locally linear supply curve 
P = a S + b

with a > 0 (i.e. upward sloping) by the quantity supplied, so we get

P × S = a S² + b S

Or in both directions:

P₁ × S₁ + P₂ × S₂ = a₁ S₁² + b₁ S₁ + a₂ S₂² + b₂ S₂

with a₁  and a₂  >  0 which is locally a paraboloid. Therefore the statements
P₁ = a₁ S₁ + b₁
P₁ × S₁ + P₂ × S₂ = a₁ S₁² + b₁ S₁ + a₂ S₂² + b₂ S₂
are not logically independent. A "bowed out PPF" defines supply curves as upward sloping, and upward sloping supply curves defines the PPF as bowed out. A bowed PPF curve doesn't "explain" the supply curve any more than non-Euclidean geometry "explains" why the parallel postulate fails.
Now I think Rowe could mean that the bowed PPF curve is more intuitive than an upward-sloping supply curve -- and that I would completely agree with. Trying to explain why a supply curve slopes up is hard. Suggesting that the PPF might bow out? Easy. Think of filling exploring a state space with a random walk maybe with occasional jumps (instead of occupied, think visited) [1]:

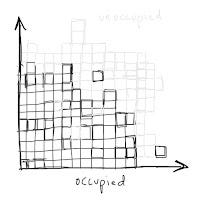
Would exploring this space look more like a triangle, a bowed-out curve or bowed-in curve? You'd probably say "it depends" and you'd be right. But the choice that requires the least amount of additional assumptions is bowed-out (think of it as a quarter of a random walk starting at zero in an 2-dimensional space). The triangle essentially requires a budget constraint, and the bowed-in curve requires a reason to prefer the axes. If we think of this as two in n >> 1 dimensions, then the most likely place to find the "explorer" is near the PPF at the surface (since most points of a higher dimensional volume are near its surface) -- with a radius essentially given by the diffusion constant D.
I'll see if that works out with some numerical simulations in a future post. But that would explain why the supply curve slopes up: diffusion from zero leads to a circular regions bounded by the PPF with radius ~ √(D t), which is equivalent to an upward sloping supply curve.
...

Footnotes

[1] My extra explanations (visited vs occupied, jumps) are here just so I could re-purpose this figure I drew for what was going to be a purely MaxEnt description of the PPF -- which is a bit harder than I originally thought. You shouldn't think of the states inside the PPF as "occupied" (as in the diagram), but rather "explored". It is sketched out above, though.