Production possibilities and Brownian motion

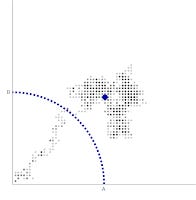
At the end of the previous post, I discussed how a bowed-out [1] production possibilities frontier (PPF) could arise from essentially Brownian motion -- and I mentioned that I'd do a simulation to demonstrate that idea. I took random paths (of length 1000) that correspond to king moves on an infinite chessboard, starting in the bottom left corner. These paths look like this (we'll get to the blue line, but the blue dot represents the average end point ... and for one path, that is just the end point):

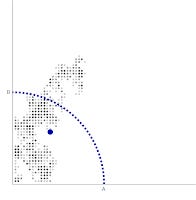
What is the average end point of 1000 paths?

The average end point seems to coincide with that blue line -- that's because it's the diffusion length D for 1000 time steps of a random walk with a step size of (roughly) unit length. You don't need to worry about the fact that one of the steps sizes is ~ 1.4. Anyway, the level curves of the (smoothed) density histogram for the end points are bowed out (the diffusion length is roughly the level curve corresponding to the mean value of the end point):

So we'd generally expect a two-good economy to be approximately the diffusion length D away from the origin [2]. Since this is a radius, this forms a set of points (PPF) that is bowed-out relative to the line between (D, 0) and (0, D).
Note that if there was some kind of constraint -- e.g. budget constraint B -- that was close to D, it could have some impact on the shape of the level curves. If B >> D, then there is little impact and D determines the PPF; if B << D, then B determines the PPF. Additionally, there could be reasons that the diffusion might favor movement parallel to the axes, resulting in a "bowed-in" PPF (e.g. economies of scale).
But without other considerations or constraints, the default should be bowed-out PPFs and upward sloping demand supply curves.
...

Footnotes

[1] By "bowed-out", we mean what Nick Rowe means. Bowed-out PPFs mean upward sloping supply curves.
[2] If diffusion was asymmetric, you'd end up with an asymmetric diffusion length and quarter-ellipse PPFs.