Miracles

Scott Sumner has a review of the Rethinking Macroeconomics conference in which he says:

On the negative side, I was extremely disappointed by some of the comments on monetary policy. In response to calls for a higher inflation target to avoid the zero bound problem, Jeremy Stein of Harvard University asked something to the effect "What makes you think the Fed can achieve higher inflation?" (Recall that Stein was recently a member of the Federal Reserve Board.) I was pleased to see Olivier Blanchard respond that there is no doubt that we can achieve 4% inflation, or indeed any trend inflation rate we want. But then Larry Summers also suggested that he shared Stein's doubts (albeit to a lesser extent.) 

I kept thinking to myself: Why do you guys think the Fed is currently engaged in steadily raising the fed funds target? What do you think the Fed is trying to achieve? How can a top Fed official not think the Fed could raise its inflation target during a period when we aren't even at the zero bound? Why has the US averaged 2% inflation since 1990---is it just a miracle?

I've addressed almost this exact statement before (with what is going to be less derision), but the emphasized sentence is either the most innumerate claim I've ever seen from a PhD economist or just an incredibly disingenuous one ... to the point of lying on purpose to deceive.

I tried to select the data series that makes Sumner's claim as close to true as possible. It requires headline PCE inflation, but regardless of the measure you use, you get the same result I will illustrate below.

Why does Sumner choose 1990? Well, it is in fact the only year that makes his claim true:

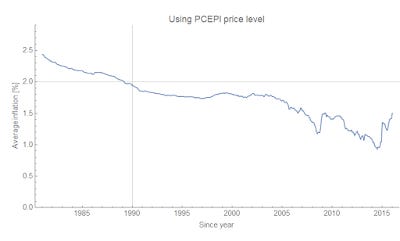
For later starting years, average inflation is lower; for earlier starting years, average inflation is higher. In fact, average inflation since year Y has been almost monotonically decreasing as a function of Y. Therefore, since it was higher than 2% at some time in the past, the statement "inflation has averaged 2% since Y = Y₀" is true for some Y₀ (and since it is almost monotonic, there is only one such Y₀). It just so happens Y₀ ≈ 1990. There's a miracle all right — but the miracle is that Sumner would pick 1990, not that the Fed would pick 2%. I'm more inclined to believe Sumner chose 1990 in order to keep his prior that the Fed can target whatever inflation rate it wants while the Fed says it's targeting 2% [1].
The other possibility here (Occam's razor) is that inflation is just falling and the Fed has no control over it [2]. But regardless of what is actually happening, Sumner is either fooling himself or others with this "evidence". And as we add more data to this series, unless PCE inflation starts to come in above 2%, Sumner's claim is going to eventually become wrong [3]. Will he reconsider it then? 
This kind of numbers game is really upsetting to me. It is the inflation equivalent of the statements by global warming deniers that there's been "no statistically significant warming since 1997" (which uses the fact that a large volcanic eruption caused temperatures to not rise for a few years, and additionally is playing a rather loose game with the words 'statistically significant' — at the time they were making that claim there wasn't enough data to say any increase was statistically significant unless it was huge).
I know: Hanlon's razor. But in the case of global warming deniers it was a deliberate attempt to mislead.
...

Footnotes:

[1] Somewhere, I don't remember where (possibly Tim Duy?) noticed that the Fed seems to actually be looking at average headline inflation of 2%, which would mean that Sumner should choose 2005 instead of 1990. 
[2] In fact, I think it might be a demographic effect. There is a period of "normal" core PCE inflation of 1.7% in the 1990s:

[3] My estimate says it'll be some time after 2020 for most plausible paths of inflation.