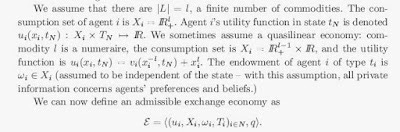Mathiness in modern monetary theory
Simon Wren-Lewis sends us via Twitter to Medium for an exquisite example of my personal definition of mathiness: using math to obscure rather than enlighten.
Here's the article in a nutshell:
Any proposed government policy is challenged with the same question: “how are you going to pay for it”.
The answer is: “by spending the money”.
Which may sound counter intuitive, but we can show how by using a bit of mathematics.
[a series of mathematical definitions]
And that is why you pay for government expenditure by spending the money [1]. The outlay will be matched by taxation and excess saving to the penny after n transactions.
Expressing it using mathematics allows you to see what changing taxation rates attempts to do. It is trying to increase and decrease the magnitude of n — the number of transactions induced by the outlay. It has nothing to do with the monetary amount.
I emphasized a sentence that I will go back to in the end. But first let's delve into those mathematical definitions, shall we? And yes, almost every equation in the article is a definition. The first set of equations are definitions of initial conditions. The second is a definition of the relationship between $f$ and $T$ and $S$. The third set of equations define $T$. The fourth defines $S$. The fifth defines $r$. The sixth defines the domain of $f$, $T$, and $S$. Only the seventh isn't a definition. It's just a direct consequence of the previous six as we shall see.
The main equation defined is this:
$$
\text{(1) }\; f(t) \equiv f(0) - \sum_{i}^{t} \left( T_{i} + S_{i}\right)
$$
It's put up on the top of the blog post as if it's $S = k \log W$ on Boltzmann's grave. Already we've started some obfuscation because $f(0)$ is previously set to be $X$, but let's move on. What does this equation say? As yet, not much. For each $i < t$, we take a bite out of $f(0)$ that we arbitrarily separate into $T$ and $S$ which we call taxes and saving because those are things that exist in the real world and so their use may lend some weight to what is really just a definition that:
$$
K(t) \equiv M - N(t)
$$
In fact we can rearrange these terms and say:
$$
\begin{align}
f(t) \equiv & f(0) - \sum_{i}^{t} T_{i} - \sum_{i}^{t} S_{i}\\
f(t) \equiv & M - T(t) - S(t)\\
K(t) \equiv & M - N(t)
\end{align}
$$
As you can probably tell, this is about national income accounting identities. In fact, that is Simon Wren-Lewis's point. But let's push forward. The article defines $T$ in terms of a tax rate $0 \leq r < 1$ on $f(t-1)$. However, instead of defining $S$ analogously in terms of a savings rate $0 \leq s < 1$ on $f(t-1)$, the article obfuscates this as a "constraint"
$$
f(t-1) - T_{t} - S_{t} \geq 0
$$
Let's rewrite this with a bit more clarity using a savings rate, substituting the definition of $T$ in terms of a tax rate $r$:
$$
\begin{align}
f(t-1) - r_{t} f(t-1) - S_{t} & \geq 0\\
(1- r_{t}) f(t-1) - S_{t} & \geq 0\\
s_{t} (1- r_{t}) f(t-1) & \equiv S_{t} \; \text{given}\; 0 \leq s_{t} < 1
\end{align}
$$
Let's put both the re-definition of $T_{i}$ and this re-definition of $S_{i}$ in equation (1), where we can now solve the recursion and obtain
$$
f(t) \equiv f(0) \prod_{i}^{t} \left(1-r_{i} \right) \left(1-s_{i} \right)
$$
This equation isn't derived in the Medium article (and it really doesn't simplify the recursive equation without defining the savings rate). Note that both $s_{i}$ and $r_{i}$ are positive numbers less than 1. There's an additional definition that says that $r_{t}$ can't be zero for all times. Therefore the product of (one minus) those numbers is another number $0 < a_{i} < 1$ (my real analysis class did come in handy!) so what we really have is:
$$
\text{(2) }\; f(t) \equiv f(0) \prod_{i}^{t} a_{i}
$$
And as we all know, if you multiply a number by a number that is less than one, it gets smaller. If you do that a bunch of times, it gets smaller still.
In fact, that is the content of all of the mathematical definitions in the Medium post. You can call it the polite cheese theorem. If you put out a piece of cheese at a party, and if people take a non-zero fraction of it each half hour, those pieces will get smaller and smaller but eventually there is nothing left (i.e. somebody takes the last bit of cheese when it is small enough). Which is to say for $t \gg 1$ (with dimensionless time) $X \equiv T + S$ because $f(t) = 0$ with $t \gg 1$.
But that's just an accounting identity and the article just obfuscated that fact by writing it in terms of a recursive function. Anyway, I wrote it all up in Mathematica in footnote [2].
Now back to that emphasized sentence above:
Expressing it using mathematics allows you to see what changing taxation rates attempts to do.
No. No it doesn't. If I write $Y = C + S + T$ per the accounting identities, then a change in $T$ by $\delta T$ means [3]
$$
\delta Y = \left( \frac{\partial C}{\partial T}+ \frac{\partial S}{\partial T} + 1 \right) \delta T
$$
Does consumption rise or fall with increased taxation rates? Does saving rise or fall with increased taxation rate? Whatever the answer to those questions are, they are either models or empirical regularities. The math just helps you figure out the possibilities; it doesn't specify which occurs (for that you need data). The Medium article claims that all that changes is how fast $f(t)$ falls (i.e. the number of transactions before it reaches zero). However that's just the consequence of the assumptions leading to equation (2). And those assumptions represent assumptions about $\partial C/\partial T$ (and to a lesser extent $\partial S/\partial T$). Let's rearrange equation (3) and use $G = T + S$ [4]:
$$
\begin{align}
\delta Y = & \frac{\partial C}{\partial T}\delta T + \frac{\partial S}{\partial T}\delta T + \delta T \\
\delta Y = & \frac{\partial C}{\partial T}\delta T + \frac{\partial G}{\partial T}\delta T \\
\delta Y = & \frac{\partial C}{\partial T}\delta T + \delta G
\end{align}
$$
And there's where we see the obfuscation of original prior. In the medium article, $f(0) = X$ is first called the "initial government outlay". It's $\delta G$. However, later $f(t-1)$ is called "disposable income". That is to say it's $\delta Y - \delta T$. However those two statements are impossible to reconcile with the accounting identities unless $X$ is the initial net government outlay, meaning it is $\delta G - \delta T$. In that case we can reconcile the statements, but only if $\partial C/\partial T = 0$ because we've assumed
$$
\begin{align}
\delta Y - \delta T & = \delta G - \delta T\\
\delta Y & = \delta G
\end{align}
$$
This was a long journey to essentially arrive at the prior behind MMT: government spending is private income, and government spending does not offset private consumption. It was obfuscated by several equations that I clipped out of the quote at the top of this post. And you can see how that prior leads right to the "counterintuitive" statement at the beginning of the quote:
Any proposed government policy is challenged with the same question: “how are you going to pay for it”.
The answer is: “by spending the money”.
Which may sound counter intuitive, but we can show how by using a bit of mathematics.
No, you don't need the mathematics. If government spending is private income, then (assuming there is only a private and a public sector) private spending is government "income" (i.e. paying the government outlay back by private spending).
Now is this true? For me, it's hard to imagine that $\partial C/\partial T = 0$ or $\delta Y = \delta G$ exactly. The latter is probably a good approximation (effective theory) at the zero lower bound or for low inflation (it's a similar result to the IS-LM model). For small taxation changes, we can probably assume $\partial C/\partial T \approx 0$. Overall, I have no real problem with it. It's probably not a completely wrong collection of assumptions.
What I do have a problem with, however, is the unnecessary mathiness. I think it's there to cover up the founding principle of MMT that government spending is private income. Why? I don't know. Maybe they don't think people will accept that government spending is their income (which could easily be construed as saying we're all on welfare)? Noah Smith called MMT a kind of halfway house for Austrian school devotees, so maybe there's some residual shame about interventionism? Maybe MMT people don't really care about empirical data, and so there's just an effluence of theory? Maybe MMT people don't want to say they're making unfounded assumptions just like mainstream economists (or anyone, really) and so hide them "chameleon model"-style a la Paul Pfleiderer.
Whatever the reason (I like the last one), all the stock-flow analysis, complex accounting, and details of how the monetary system works serve mainly to obscure the primary point that government spending is private income for us as a society. It's really just a consequence of the fact that your spending is my income and vice versa. That understanding is used to motivate a case against austerity: government cutting spending is equivalent to cutting private income. From there, MMT people tell us austerity is bad and fiscal stimulus is good. This advice is not terribly different from what Keynesian economics says. And again, I have no real problem with it.
I'm sure I will get some comments that say I've completely misunderstood MMT and that it's really about something else. But please don't forget to tell us all what that "something else" is. But the statement here that "money is a tax credit" plus accounting really does say, basically, that government spending is our income.
But with all the definitions and equations, it ends up looking and feeling like this:
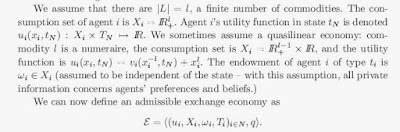
There seems to be a substitution of mathematics for understanding. In fact, the Medium article seems to think the derivation it goes through is necessary to derive its conclusion. But how can a series of definitions lead to anything that isn't itself effectively a definition?
Let me give you an analogy. Through a series of definitions (which I have done as an undergrad math major in that same real analysis course mentioned above), I can come to the statement
$$
\frac{df(x)}{dx} = 0
$$
implies $x$ optimizes $f(x)$ (minimum or maximum). There's a bunch of set theory (Dedekind cuts) and some other theorems that can be proven along the way (e.g. the mean value theorem). This really tells us nothing about the real world unless we make some connection to it however. For example, I could call $f(x)$ tax revenue and $x$ the tax rate ‒ and adding some other definitions ($f(x) > 0$ except $f(0) = f(1) = 0$) and say that the Laffer curve is something you can clearly see if you just express it in terms of mathematics.
The thing is that the Laffer curve is really just a consequence of those particular definitions. The question of whether or not it's a useful consequence of those definitions depends on comparing the "Laffer theory" to data.
Likewise, whether or not "private spending pays off government spending" is a useful consequence of the definitions in the Medium article critically depend on whether or not the MMT definitions used result in a good empirical description of a macroeconomy.
Without comparing models to data, physics would just be a bunch of mathematical philosophy. And without comparing macroeconomic models to data, economics is just a bunch of mathematical philosophy.
...
Update 5 May 2017:
Here's a graphical depiction of the different ways an identity $G = B + R$ can change depending on assumptions. These would be good pictures to use to try and figure out which one someone has in their head. For example, Neil has the top-right picture in his head. The crowding out picture is the bottom-right. You could call the picture on the bottom-left a "multiplier" picture.

Update 6 May 2017: Fixed the bottom left quadrant of the picture to match the top right quadrant.
...
Footnotes:
[1] "And that's why I don't like cricket." [YouTube]
This is basically equivalent to what is done in the Medium article.
[2] Here you go:


[3] If someone dares to say something about discrete versus continuous variables I will smack you down with some algebraic topology [pdf].
[4] I think people who reason from accounting identities seem to make the same mistakes that undergrad physics students make when reasoning from thermodynamic potentials. Actually, in the information equilibrium ensemble picture this becomes a more explicit analogy.