Mathiness and the Solow production function
Mark Thoma sends us to Paul Romer's blog post about his paper that defines "mathiness" in economics research -- in particular in growth economics:
The style that I am calling mathiness lets academic politics masquerade as science. Like mathematical theory, mathiness uses a mixture of words and symbols, but instead of making tight links, it leaves ample room for slippage between statements in natural versus formal language and between statements with theoretical as opposed to empirical content.
I think there is no better place to see this than the Solow growth model's Cobb-Douglas production function. A really pure dose of the mathiness can be seen here at MR University. In it, they motivate the equation
$$
Y = A \; K^{\alpha} \; L^{1 - \alpha}
$$
where $Y$ and $K$ are real quantities. First, why are they real quantities? I've never quite found a good answer, but in general most economists think that the price of bread being twice as much as it was decades ago is something that should be adjusted for (taken out of the values), not a fundamental property of economics. Of course, solving that problem (by adjusting for inflation) creates a new problem -- money illusion (why do humans seem to think in nominal terms). Usually when incorporating an idea creates new problems, it's a sign that maybe the idea isn't right. But adjusting for inflation is well-established, so let's not rock the boat too much. Besides, there's other examples we can use.
Second, $A$ (total factor productivity, TFP) is introduced on the MRU videos as representing something that exists in the real world: "ideas" or productivity. It's not just a normalization factor. It also implies that it can change over time or across countries. We are immediately assuming that instead of an unimportant normalization that is constant over time, we have a critical component of growth economics.
Finally, while there are potentially reasons for the constant returns to scale assumption where the exponents of $K$ and $L$ add to 1 -- Alex Tabarrok states it in terms of doubling $K$ and $L$ should lead to a doubling of output -- it represents an additional assumption. In most cases, however, the reason for the assumption is a theoretical reason, not empirical.
Actually, we've made three major assumptions before comparing to empirical data: real quantities $Y$ and $K$, $A$ is a factor of production and constant returns to scale for $L$ and $K$. These assumptions lead to $A$ (the normalization factor in your original model) being the most important thing in growth economics -- it represents most of economic growth. Additionally, the model using these assumptions are used to make the assertion (explicitly in the MRU video, but generally the conclusion in much of growth economics) that Mexico doesn't use its labor or capital as effectively as the US.
Note that the theoretical assumptions create these new mysteries: 1) why is most growth TFP and 2) why do some countries use capital and/or labor better than others.
Now in the much more general information equilibrium approach, we end up with almost the same Solow production function
$$
Y = A \; K^{\alpha} \; L^{\beta}
$$
but without the three assumptions. $Y$ and $K$ could be nominal or real quantities, $A$ is a normalization factor that mostly represents the units of $K$ and $L$, and $\alpha$ and $\beta$ are completely arbitrary. What do we get if we compare this model to empirical data? Almost perfect agreement:
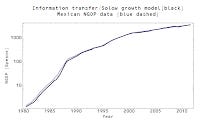
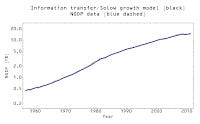


That's for the US and Mexico, using nominal quantities for $Y$ and $K$. $A$ is just a normalization factor and not responsible for any economic growth. In Mexico, $\alpha + \beta \simeq 1.42$ with $\alpha \simeq 0.90$ and $\beta \simeq 0.51$. In the US, $\alpha + \beta \simeq 1.25$ with $\alpha \simeq 0.85$ and $\beta \simeq 0.40$. We draw the exact opposite conclusion as MRU: Mexico grows much faster than the US for a given (relative) input of capital or labor!
This may even resolve another conundrum created by the Solow growth model -- why would the US or other advanced countries invest in Mexico if productivity was higher in the US? Sure, maybe the stock of capital is low and so you get more growth relative to depreciation -- but again that is entirely because of the way the Solow production function is built! In the information equilibrium framework, we see that increases in capital grow the economy a bit more than in the US (the exponent is 0.90 vs 0.85). Why move your labor intensive manufacturing to Mexico? Fractionally increasing labor in Mexico produces fractionally more output than in the US (the exponent is 0.51 vs 0.40). I am thinking that "productivity" may just be a way to preserve the idea that the US economy is the best in the world ... a way steeped in mathiness. And maybe even racism.
Note that making the overall normalization $A$ an important factor and using "real" quantities basically transforms the scale of the unit of account an important property of economic growth. The fact that it's ~ 100 Yen or ~ 10 pesos that is roughly equivalent to 1 US dollar or 1 Euro (completely arbitrary designations) is turned into an important economic fact about productivity -- at least if the information equilibrium view is correct.
If you look at the Solow production function empirically and scientifically, you end up with a pretty simple model that works remarkably well! If you try to add assumptions, you end up having to live with added mysteries and a much more complex model -- that doesn't even work that well. Call it Occam's razor, or call it rooting out mathiness. Just be curious -- why do we make certain assumptions?
Update +15 min: The rather large NGDP growth of Mexico in the 1980s is the result of hyperinflation. The nuevo peso was introduced in 1993, shaving off three zeros from prices. Also added the (relative) in the paragraph after the graphs.



