Jason versus the Fed

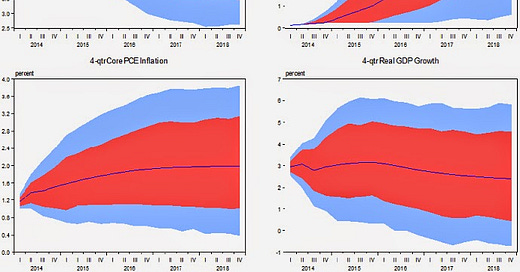
A few months ago I learned from Noah Smith's blog that the Fed had released one of its models: the FRB/US model. On the linked Fed webpage, they gave an example analysis done with this model that predicted four macroeconomic variables (clockwise from the top left: the unemployment rate, the Fed funds rate -- wait, don't they set this? [1], RGDP growth and PCE inflation):

How does the (far simpler [2]) information transfer model stack up against this model? I started from the trend inflation modeled here and predicted out to the end of 2018 (the prediction bands are the 70% and 90% bands like in the Fed model, based on a Gaussian error distribution -- which if you check the link is a pretty good model):

I was unable to find numerical data for the Fed's prediction, so I rather cheesily traced out the central value and the error bands in PowerPoint (in red) and placed them on top of a close up of the prediction in the previous graph:

The overall error at the end of the period seems about the same (recall that for short term predictions, the information transfer model is pretty much dominated by measurement error, not model error). It is kind of funny that the first few measurements after the start of the prediction jump right outside the Fed's 90% confidence interval. The interesting thing is that these models predict different things -- although given the overlap of the 70% confidence interval, there is a strong possibility of failing to reject either model (i.e. both are fair descriptions).
I'll keep updating this as inflation data becomes available.
For a bonus graph, here is the model result without the smoothing:

Footnotes:

[1] Just kidding.

[2] According to the Fed website, "FRB/US currently contains about 60 stochastic equations, 320 identities, and 125 exogenous variables" ... of course it models quite a bit more (like household consumption and savings).