Is information transfer economics hard?
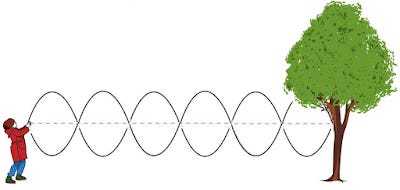
The basic premise of information transfer economics: if I shake one end of a jump rope tied to a tree in Morse code, the tree feels a force that can be used to reproduce my input signal. If I shake NGDP in Morse code, hours worked should fluctuate in such a way to get that pattern back out. Image from Wikimedia Commons.
I admit I have trouble understanding what others find so difficult about the information transfer framework for economics. For example, Scott Sumner writes:
But he [meaning me] went even further than the other two [Matt Yglesias and Britmouse], creating a revolutionary new type of economics called “Information Transfer Economics.” Although I’ve tried to understand his model, it’s all way over my head. He knows a lot more math than I do.
I'm pretty sure Sumner was being sarcastic when he called it 'revolutionary'. However, Sumner actually writes down an information equilibrium [1] model on his blog for what he considers to be his own model. In this post we have an hours worked delta (from a "natural rate") related to an NGDP delta (from a future market or central bank target). The key point to understanding the information equilibrium view is to see fluctuations aggregate demand transmitting a signal to hours worked -- i.e. a wiggle in NGDP shows up as a wiggle in H.
$$
\frac{NGDP - NGDP^{T}}{H - H^{n}} = \frac{\Delta NGDP}{\Delta H} = \alpha ' \frac{NGDP}{H}
$$
This is effectively the information equilibrium model:
$$
NGDP \rightarrow H
$$
$$
\frac{dNGDP}{dH} = \alpha ' \frac{NGDP}{H}
$$
with the equation just being what the notation $NGDP \rightarrow H$ is shorthand for. Sumner would assume (in the information transfer framework) that the ratio $NGDP^{T}/H^{n}$ is roughly constant (a good approximation over the short run) and is subsumed into his constant $\alpha$.
There is also his plot of the ratio of hourly nominal wages to NGDP versus the unemployment rate. This appears to be the information transfer model:
$$
u: NGDP \rightarrow NHW
$$
Of course, the more empirically accurate version (in both cases) is
$$
P : NGDP \rightarrow H
$$
where P is the price level, which is essentially Okun's law.
What I can only assume are economics students on EJMR appear to get the general concept even when they don't understand everything else:
I could never figure out what he was doing.
He says things like my model is Y~X, where that stands for some large class of (linear?) models. ...
I'd have said log-linear instead of linear (which I'm sure the person meant, but just to make it clear to everyone else), but basically, yes, that's it. I'd write $Y \sim X$ for information equilibrium and $Y \rightarrow X$ for information transfer ... and add a "detector", an abstract "price" $p$ in economics parlance so that $p : Y \rightarrow X$
It's a severe restriction if your initial range of choices includes anything your heart desires, but for the most part lots of models fall into this class. It really is just a bare minimum requirement for how X and Y have to behave if you want to say as the economist "X and Y are related". At a bare minimum -- if you say X and Y are related -- wiggling X has to wiggle Y to some degree. If you sent a Morse code signal by changing X, you should be able to read it at Y.
The biggest difference from mainstream approaches is in the interpretation. In the traditional economic view, permanently increasing the monetary base causes agents to expect higher inflation, so the price level rises. In the information transfer view increasing the monetary base makes higher price level states more likely (most of the time) and agents end up in a state such that we observe higher inflation.
It makes the language a lot more passive. Agents "end up" working more hours or accepting higher prices for bacon. Why do they end up in those situations? That's a really hard problem. A single mother might take on a couple of hours a week more than she wants because she's covering for a colleague that left for a new full time job and thinks her manager would appreciate it. Total hours increase, say, from 20 + 20 = 40 to 22 + 40 = 62. Predicting that extra 2 hours would be a nightmare in terms of an agent based model (a utility calculation based on the single mother's time she wants to spend with her kid, expenses for child care, transportation costs, and how much she thinks her manager would appreciate x extra hours). Information equilibrium just tells us that somehow all those extra hours from monetary or fiscal stimulus (depending on the model) get allocated. The details of the process for each individual agent go into the coefficient $\alpha$ in the equations above.
In that sense, information transfer economics is much easier than traditional economics. It also becomes a much more empirical framework. If I say M1 is the source of all fluctuations in NGDP, then we should have an information equilibrium relationship (for some $k$):
$$
\frac{dNGDP}{dM1} = k \; \frac{NGDP}{M1}
$$
If this isn't true empirically, then there is something missing in your model.
Footnotes:
[1] I try to say information transfer model for the general case and where we allow non-ideal information transfer -- $I(D) \geq I(S)$ -- and information equilibrium model for cases where information transfer is ideal -- $I(D) = I(S)$.