Dynamic information equilibrium model of initial claims

Weekly initial unemployment insurance claims (ICSA) were put up on FRED today, and so I thought I'd apply the dynamic information equilibrium model to the data. First, we need to divide by the size of the Civilian Labor Force (CLF) per the model $ICSA \rightleftarrows CLF$ in order to observe the ratio such that:
$$
\frac{d}{dt} \log \frac{ICSA}{CLF} \approx (k-1) r + \sum_{i} \sigma_{i}(t) \equiv \alpha + \sum_{i} \sigma_{i}(t)
$$

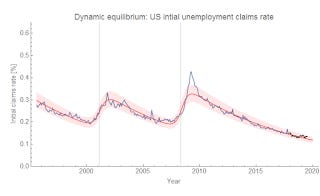
For the data since the mid-90s, there are two shocks $\sigma_{i}(t)$ corresponding to the early 2000s recession and "the Great Recession". The forecast, conditional on the absence of shocks (detectable e.g. via this algorithm), calls for a continued fall in the initial claims rate:

The dynamic equilibrium rate $\alpha$ is −0.103/y (that is to say roughly a 10% relative fall per year — e.g. a 1% initial claims rate would fall by 0.1 percentage points to 0.9%). I'll continue to follow this forecast in the new year.

...

Update 1 August 2019

lol. I never did track this one until today (a year and a half later). It did fine — here's the original graph and a zoomed-in version: