Consumption, income, and wealth
John Handley has started up a new updated blog, and the most recent post asks an interesting question (in a way that should be lauded for both its use of data and making the code available): if disposable income predicts consumption so well (i.e. the traditional Keynesian consumption function), why did anyone start using the Euler equation with its "almost comical level of inaccuracy"? While we wait for the optimal answer to that question from Beatrice Cherrier, my intuition says the answer is "microfoundations". John asked me to verify his regressions, which I did; the model he considered has the added benefit of being an information equilibrium model so I am writing it down here.
The basic Keynesian consumption function is essentially a linear model
PCE = a DPI + c
where PCE is personal consumption (FRED PCEC) and DPI is disposable income (FRED DPI). However John discovered an excellent relationship between PCE, DPI and total net worth (FRED TNWBSHNO) which I will call TNW for short:
log PCE = a log DPI + b log TNW + c
This has the form of an information equilibrium relationship (as well as a Cobb-Douglas production function where income and wealth are both "factors of production" for consumption):
PCE ⇄ DPI
PCE ⇄ TNW
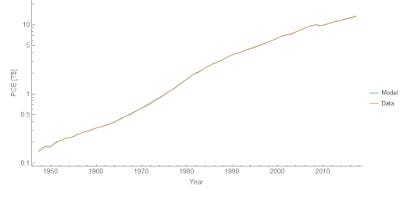
with information transfer indices a and b. It also reduces to the basic Keynesian model in the limit where changes in TNW and DPI are small (in percentage terms). The model works pretty well [1]:
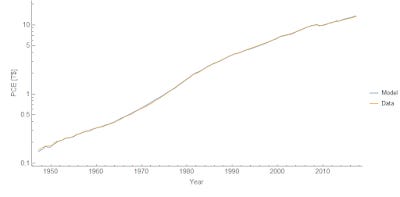

We find a = 0.82, b = 0.18, and c = -0.47. This result has several different implications. First, as John's says via Twitter, it means "consumers are way more hand to mouth than typical model[s] suggest". It also suggests that changes to income have a bigger impact on consumption than equivalent relative changes in wealth. Note that a ~ 1 means that the permanent income hypothesis isn't a good approximation (which requires a << 1) in line with previous results using information equilibrium to describe lifetime income and shocks to income. Additionally, including different methods [1] as well as John's results, the result nearly always gave a + b ≈ 1, i.e. constant returns to scale.
Overall, this is a pretty good model of consumption in terms of income and wealth.
...
Update + 3 hours
One thing to note is that the empirical finding that a + b ≈ 1 implies that there is a constant wealth-to-income ratio (for the same reasons the labor share is constant in the Solow model). This lends credence to the frequent stock-flow consistent model assumption of a constant wealth-to-income ratio (possibly subjected to stochastic shocks per the dynamic equilibrium model).
...
Update + 4.5 hours
Despite lauding John Handley above for making his code available, I forgot to upload the Mathematica code for the model to the repository (information equilibrium). This has been rectified.
...
Footnotes:
[1] I tried multiple different ways of estimating the parameters and all give approximately comparable results (and comparable to John's results as well).