Comparing methodologies (monetary base and short term interest rates)

In the process of setting up the Granger-causality test of the relationship between the monetary base (St. Louis Adjusted monetary base) and short term interest rates (3 month secondary market rate) mentioned here, but I thought there should be a quick aside on something Mark Sadowski said:

... if a time series model’s results are reported without routine references their statistical significance, then they should always be viewed with deep skepticism. ...

... an argument consisting of little more than a line graph depicting the time series of values of a quantity should never be accepted as a proof of anything, except that the person who is arguing that it proves something is not familiar with what constitutes acceptable empirical evidence, is incapable of understanding what constitutes acceptable empirical evidence, or is simply willfully ignoring what constitutes acceptable empirical evidence because it contradicts their preferred model.

Almost zero theoretical physics papers pay attention to statistical significance in this way. Obviously physics is "doing it wrong" and that's why the field is in a state of existential methodological crisis. Oh, wait. That's economics.

Personally, I'd say any statistical results presented without reference to an explicit model means that an implicit model has been used -- and you treat any implicit results with deep skepticism.

As Paul Krugman says:

Any time you make any kind of causal statement about economics, you are at least implicitly using a model of how the economy works. And when you refuse to be explicit about that model, you almost always end up – whether you know it or not – de facto using models that are much more simplistic than the crossing curves or whatever your intellectual opponents are using.

Here's an example where you can see this at work ... first setting up the data

The next bit looks for the best single lag to compare the first differences of the two time series (in both directions) ...

This is a basic fit with a single lag ...

It works pretty well for an economic model (changes short term interest rates cause changes in the monetary base: rates go down, base goes up ...)

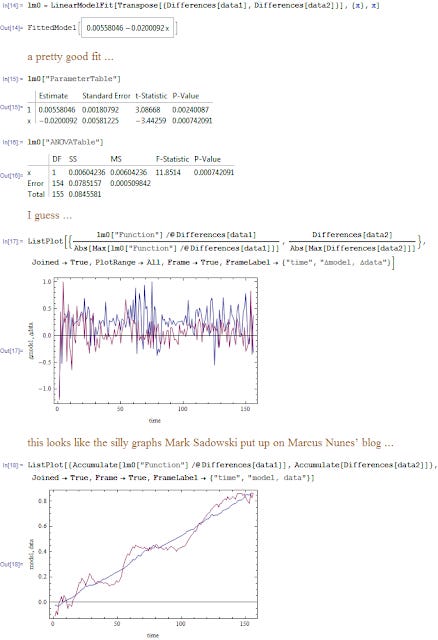
How about the same thing but looking at levels? Well the traditional stats test is going to be garbage because of spurious correlation ... but the model looks much better than the statistically "proper" version ...

Does a slavish devotion to statistical purity lead us away from real understanding?