Because empirical success

I've occasionally had discussions with some commenters, most recently Philippe on this thread, that such and such explanatory variable can't possibly be used to explain what I'm trying to explain because it doesn't make sense to that commenter. In the recent case, Philippe suggested that it didn't make sense that physical currency (the currency component of the monetary base, which I call M0) was an explanatory variable for inflation. Philippe suggested other forms of money that should matter for inflation, like M1 or central bank reserves.

You could probably put the brief back and forth between Nick Rowe and myself in the previous few posts into this framework, except in that case I'm disagreeing with Nick by saying expectations (the explanatory variable) can't explain the price level or inflation. Nick suggests that expectations (and central bank targets or guidance) are an explanatory variable, while I'm saying expectations do not explain much more than the most recent NGDP and M0 numbers.
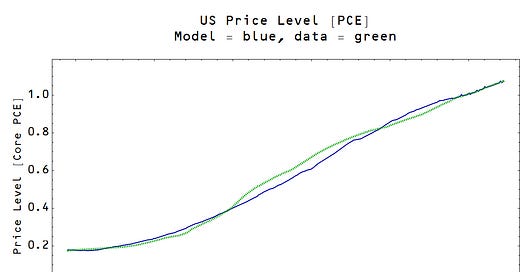
Maybe the information transfer model is wrong and expectations and M1 matter for inflation. Whatever model you have, though, it can't be too different from the ITM. Why? Because empirical success. Here are the information transfer model results for the price level and inflation. First, here they are for the core PCE measure:

And here are the results for core CPI:

This is more empirically successful than any economic model of inflation that has ever been published. The P* model from the Federal Reserve was comparable in the 1990s, but choked on new data. Maybe the ITM will choke on new data, too. However, time and data will tell, not theoretical arguments. The details of the model are all written down in the "for beginners" posts linked on the sidebar of this blog. Have a go yourself! All of the data I've used is from FRED (except the Japanese monetary base data, which is from here).
Also note that the fact that both fits are good means that core PCE and core CPI inflation are not independent measures. The information transfer model describes them both equally well given the data we have, so there is no telling which is the "real" measure of inflation. What is interesting is that this observation follows regardless of whether you believe the information transfer model or not. The ITM fit to each measure implicitly defines a global transformation you can perform to turn CPI data into PCE data meaning that PCE = f(CPI) so that any property of CPI can be mapped to a property of PCE. The next time you see an economist chide someone for confusing the two measures, you can come to the rescue with the retort: there is no economically meaningful difference in PCE or CPI inflation. It's like the fact that there is no physically meaningful difference in measuring distances in kilometers or miles.
And it's not like the model for the US is a fluke; here is Japan:

The empirical accuracy doesn't mean various theoretical criticisms of the information transfer model are prima facie wrong; it just means they should be discounted (i.e. given a low prior probability of being correct) unless they are accompanied by a model of comparable empirical success. Or as I said to Philippe:

The benefit of using M0 as the explanatory variable for inflation is that it gives an incredibly accurate model. If you have done [sic] better model that uses M1 or MB that explains the price level, I'm interested in hearing about it! But if you're just making hand waving arguments without any empirical evidence, that seems like a step backwards from the ITM.

The ITM doesn't just do inflation -- the interest rate model is pretty good too:

If you're of the opinion that the Fed's expansion of reserves will result in inflation, that people's expectations matter, or even that human decisions and behavior matter in a macroeconomic system at all, I'd first like to see some lines going through some data points.

Update 7:30pm MST, for Nick's comment below: 

Both of the error results for the PCE and CPI inflation models above have approximately zero mean. First, PCE inflation error:

Second, CPI inflation error: