An RLC circuit with R = S and L = F

An RLC circuit is a simple electric circuit with a resistor, inductor and capacitor in it -- with resistance R, inductance L and capacitance C, respectively. It's one of the simplest circuits that displays non-trivial behavior.
You can derive an equation for the behavior by using Kirchhoff's laws (conservation of the stocks and flows of electrons) and the properties of the circuit elements. Wikipedia does a fine job.
You arrive at a solution for the current as a function of time that looks generically like this (not the most general solution, but a solution):
$$
i(t) = A e^{\left( -\alpha + \sqrt{\alpha^{2} - \omega^{2}} \right) t}
$$

with $\alpha = R/2L$ and $\omega = 1/\sqrt{L C}$. If you fill in some numbers for these parameters, you can get all kinds of behavior:

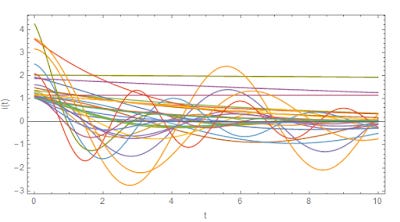
As you can tell from that diagram, the Kirchhoff conservation laws don't in any way nail down the behavior of the circuit. The values you choose for R, L and C do. You could have a slowly decaying current or a quickly oscillating one. It depends on R, L and C.
Now you may wonder why I am talking about this on an economics blog. Well, Cullen Roche implicitly asked a question:

Although [stock flow consistent models are] widely used in the Fed and on Wall Street it hasn’t made much impact on more mainstream academic economic modeling techniques for reasons I don’t fully know.

The reason is that the content of stock flow consistent modeling is identical to Kirchhoff's laws. Currents are flows of electrons (flows of money); voltages are stocks of electrons (stocks of money).

Krichhoff's laws do not in any way nail down the behavior of an RLC circuit.

SFC models do not nail down the behavior of the economy.

If you asked what the impact of some policy was and I gave you the graph above, you'd probably never ask again.

What SFC models do in order to hide the fact that anything could result from an SFC model is effectively assume R = L = C = 1, which gives you this:

I'm sure to get objections to this. There might even be legitimate objections. But I ask of any would-be objector:

How is accounting for money different from accounting for electrons?

Before saying this circuit model is in continuous time, note that there are circuits with clock cycles -- in particular the device you are currently reading this post with.

I can't for the life of me think of any objection, and I showed exactly this problem with a SFC model from Godley and Lavoie:

But to answer Cullen's implicit question -- as the two Mathematica notebooks above show, SFC models don't specify the behavior of an economy without assuming R = L = C = 1 ... that is to say Γ = 1.

Update:

Nick Rowe is generally better than me at these things.