A trivial maximum entropy model and the quantity theory

This is a trivial maximum entropy model, but I still think the result is interesting.

Let's take an economy with d = 100 dimensions subjected to a budget constraint Σ m = M(t) where t is time, m is the (randomly chosen) allocation of the total amount of money M to each dimension (these could be "markets", "firms" or even "agents"). This is effectively this picture except d = 3 here (the Ci are the dimensions):

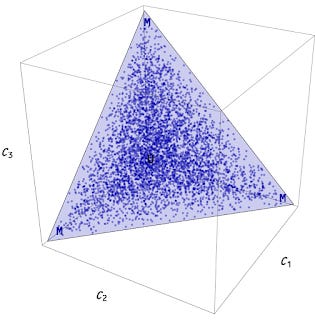
If we take the derivative of the ensemble average d/dt log 〈m〉(assuming a uniform distribution), we get something (blue paths) that roughly follows d/dt log NGDP (yellow path):

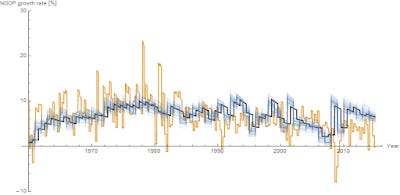
The paths obviously converge to d/dt log M (black path) ... it doesn't even depend on d because 〈m〉= α M with constant α even if we don't have d >> 1 since
d/dt log α M = d/dt (log M + log α) = d/dt log M
If d >> 1 then we have α ~ d/(d + 1) → 1, but this isn't terribly important. What this does show is that
d/dt log M ~ d/dt log NGDP
k M ~ NGDP
and we have a simplistic quantity theory of money based on randomly allocating money to different markets.