A quantity theory of labor and capital
Some of the problems with the "quantity theory of labor" is 1) it doesn't work for the UK, and 2) it underestimates RGDP.
What about the Solow model? It was very accurate as a model of NGDP. And it is accurate for UK. Let me lay out the model. Consider two simultaneous markets (employed labor and nominal capital) with core CPI being the detector in the labor market:
CPI : NGDP ⇄ L
X : NGDP ⇄ K
The X is an irrelevant price in the capital market [ed. note: actually, it's technically the capital deflator]. We can solve these markets for the general equilibrium (as in the paper):
NGDP = n0 (L/l0)ᵝ (K/k0)ᵞ
CPI ≡ dNGDP/dL = (n0/l0) β (L/l0)ᵝ⁻¹(K/k0)ᵞ
The only other detail is that I used core CPI to inflate real capital to obtain nominal capital (the result does not change much if you use e.g. the GDP deflator). Capital stock only goes until 2012 on FRED as well.
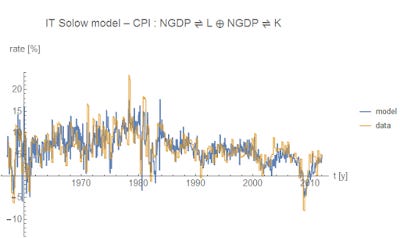
So how does this perform? In a word, brilliantly:

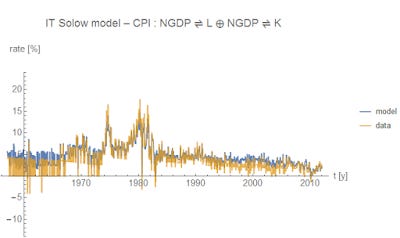
[mic drop]
[picks mic back up]
Oh, wait -- so does this help us with why the quantity theory of labor performs poorly for the UK? Yes, it does. The UK (in this model) is much more capital intensive than the US or Canada. In the US (above), we have β = 0.8 and γ = 0.7, but the UK has β = 0.5 and γ = 1.0 -- meaning the capital component contains much more of the variation.
[mic drop ... again]
[picks mic back up ... again]
Also the IT Solow model doesn't require β + γ = 1.
[mic drop ... again]
[fumbling around for the opening in the curtain]
...
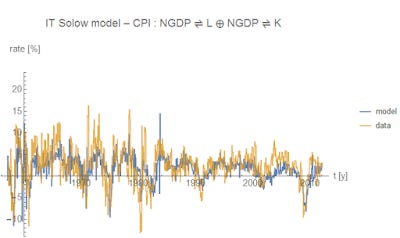
Update 17 March 2016
Commenter Marko gave me a link to the deflator for that real capital series, so here's the update to the model results ... not much change: