3/4 of a knife, 3/4 of a fork and 3/4 of a spoon

Cesar Hidalgo is looking into information theory with his new book. I haven't read it; however I have read Diane Coyle's review (H/T Mike Norman) and it seems like it might be a great source of analogies for this blog. This one immediately struck me:

Hidalgo makes the same point as the final chapter of [Diane Coyle's] GDP book, that in adding things up in terms of their monetary value we are not capturing the value of diversity: three spoons are not as valuable as a knife, fork and spoon.

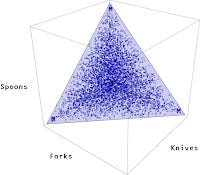
That is actually the exact point of this post here. We'll almost exactly. If we have M dollars to spend on knives, forks and spoons, (assuming they equally cost one Euro [1] WOLOG) then all consumption possibilities (blue points) are located under the budget constraint hyperplane in the first (left side) figure:

The maximum entropy point is given by the black dot in the second (right side) figure. Now for three items, that point is actually at {M/4, M/4, M/4} so if you had 4 €, you'd have 1 fork, 1 knife and 1 spoon at the maximum entropy point (and 1 € left over).

The entropy maximum is related to equilibrium in the information transfer model  as well as effectively ideal markets. Under certain (ideal) conditions, it recovers all of the properties of maximizing utility.

I would disagree with the analogy of crystallizing imagination Hidalgo uses -- that is a lower entropy state for one thing. The key idea we want to capture is Jaynes' dither. We want to make the world safe for people to move about the space of possibilities -- to try and fail.

PS This also maximizes entropy.

Update +15 minutes:

Since the maximum entropy state (3/4, 3/4, 3/4) with budget constraint M = 3 is not realizable given quantized knives, forks and spoons, you'd actually have a combination of the states (1, 1, 1), (1, 1, 0), (1, 0, 1) and (0, 1, 1) realized among a quarter of the population each.

Footnotes:

[1] I'm using Euros (€) here because the dollar symbol messes with mathjax.